Методика организации учебно-познавательной деятельности учащихся на первых уроках алгебры
В последние годы в связи с дифференциацией обучения, появлением школ и классов различной профильной направленности, в том числе гуманитарных, технических, экономических, естественно-математических и других, по-новому встают вопросы о целях, содержании, формах и методах обучения математике в школе, о месте и роли каждого школьного предмета.
Ни для кого не секрет, что на уроках математики повышается уровень умственной нагрузки, что заставляет нас задуматься над тем, как не потерять, а поддержать у учащихся интерес к изучаемому материалу на протяжении всего урока. Ведутся поиски новых методов обучения, которые способствовали бы этому. В первую очередь, надо построить урок так, чтобы каждый ученик был вовлечён в работу и, коэффициент всему прочему, эта работа должна его интересовать. Из педагогической практики мы знаем, что игру использовали, в основном, на занятиях математического кружка или во внеклассной работе. Но последнее время на уроках алгебры и геометрии всё чаще используют дидактические игры, как особую форму занятий – игровую форму .
В процессе математической деятельности учащихся в арсенале приёмов и методов мышления включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование, аналогия. Объекты математических умозаключений и правил их конструирования вскрывают механизм логических построений, вырабатывают умение формировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умения действовать по заданному алгоритму и конструировать новые в ходе решения задач. Развиваются творческая и прикладная стороны мышления.
Объект исследования данной работы – процесс обучения алгебре в 7 классе.
Предмет исследования – методика организации учебно-познавательной деятельности учащихся на первых уроках алгебры.
Цель исследования – разработка методики проведения первых уроков алгебры в 7 классе.
Задачи исследования:
Изучить учебно-методическую литературу по алгебре 7 класса;
2.Определить методические, психолого – педагогические и дидактические особенности преподавания темы, исследуемой в выпускной квалификационной работе;
3. Обосновать и разработать содержание и методику изучения материала по теме исследования.
Решение поставленных задач потребовало привлечения следующих методов исследования:
1. Анализ психолого-педагогической, математической и методической литературы, школьных программ, учебников и учебных пособий по алгебре 7 класса;
2. Беседы с преподавателями, наблюдение за учащимися 7 класса;
3. Проведение практической проверки разработанной методики.
Практическая значимость исследования определяется тем, что в нём разработаны:
1. Учебные материалы для преподавания первых уроков алгебры в 7 классе;
2. Система задач для указанной темы, в том числе: устных, опорных, стандартных, повышенной трудности, нестандартных, исследовательских;
3. Методические рекомендации для начинающих учителей и студентов педагогических ВУЗов по организации обучения по представленным материалам.
Данная тема является связующим звеном между курсом математики 5-6 классов и курсом алгебры 7 класса. Её изучение рекомендуется использовать для закрепления ранее приобретённых умений выполнять действия с рациональными числами и простейшие преобразования выражений, решать несложные уравнения, использовать аппарат уравнений для решения текстовых задач.
С определением объекта и предмета связана еще одна характеристика - проблема исследования, которая всегда должна быть направлена на определенное совершенствование выявленного предмета исследования.
Для данной дипломной работы проблемы могут быть сформулированы следующим образом:
1. Новый предмет, новое название предмет;
2. Появляется новая терминология и символика;
3. Выявление путей реализации развивающих функций в процессе изучения алгебры в 7 классе;
4. Развитие возможных путей формирования конструктивных умений и навыков учащихся в процессе обучения стереометрии на основе совершенствования содержания учебного материала.
5. Уроки должны быть построены таким образом, чтобы каждый ученик был вовлечён в работу.
Теоретические основы первых уроков алгебры в 7 классе
Выражение, состоящее из чисел, знаков действия и скобок, называется числовым выражением.
Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения.
Решим задачу:
"Туристы в течение двух часов ехали на велосипедах по шоссе со скоростью 16 км/ч, а затем шли лесом ещё 7 км. Какова длина всего маршрута?"
По шоссе туристы проехали 16·2 км, а лесом прошли 7 км. Поэтому длина всего маршрута равна (16·2+7) км, т. е. 39 км.
Решая задачу, мы получили числовое выражение 16×2+7.
Приведём ещё примеры числовых выражений:
43:5; 9,6-3×1,2; 5×(7,4-6,1).
Найдём, например, значение выражения 96-2×62. Для этого мы должны, соблюдая принятый порядок действий, сначала выполнить возведение в степень, затем умножение и, наконец, вычитание:
62=36;
2×36=72;
96-72=24.
Число 24 –значение выражения 96-2×62.
Если в выражении встречается деление на нуль, то это выражение не имеет значения, так как на нуль делить нельзя. О таких выражениях говорят, что они не имеют смысла.
Например, не имеют смысла такие выражения, как
35:(4×2-8), 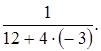
Выражение, содержащее буквенную часть, называется выражением с переменной.
Если в выражении с переменными подставить вместо каждой переменной какое-либо её значение, то получится числовое выражение. Его значение называют значением выражения с переменными при выбранных значениях переменных.
Двигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60×2 км, за 3 ч - 60×3 км, за 5ч - 60×5 км. Вообще, за t ч он пройдёт 60t км. Изменяя значение t, мы можем с помощью выражения 60t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t – выражением с переменной.
Приведём ещё пример. Пусть длины сторон прямоугольника равны a см и bсм. Тогда его площадь равна ab см2. выражение ab содержит две переменные a и b. Оно показывает, как находить площадь прямоугольника при различных значениях a и b.
Например,
a=8 и b=11, то ab=8×11=88;
a=25 и b=4, то ab=25×4=100.
функция алгебра стереометрия урок
Так, число 88 есть значение выражения ab при a=8 и b=11, число 100 есть значение этого выражения при a=25 и b=4.
Рассмотрим выражение ![]() . При любом b≠3 можно
найти его значение.
. При любом b≠3 можно
найти его значение.
Например, если
b=13, то ![]() =
=![]() =
=![]() =1,3.
=1,3.
При b=3 значение
этого выражения найти нельзя, так как в этом случае делитель b-3
равен нулю. Говорят, что при b≠3 выражение ![]() имеет
смысл, а при b=3 оно не имеет смысла.
имеет
смысл, а при b=3 оно не имеет смысла.
Некоторые выражения имеют смысл при всех значениях переменных. Примерами могут служить выражения
x(x+1), ay-4, ![]() .
.
Выражения с переменными используются для записи формул.
Рассмотрим, например, формулу четного числа. Любое четное число m можно представить в виде произведения числа 2 и целого числа n, т. е. m=2n.
Если в эту формулу вместо n подставлять целые числа, то значениями переменной m будут четные числа. Формулу m=2n называют формулой четного числа.
Формулу m=2n+1, где n- целое число, называют формулой нечетного числа.
Аналогично формуле четного числа можно записать формулу числа, кратного другому натуральному числу.
Например, формула числа, кратного 3, запишется так: m=3n, где n-целое число.
Для любых двух числовых выражений можно установить, равны их значения или нет, и если они не равны, то какое из них больше и какое меньше.
Результат сравнения значений выражений можно записать в виде равенства или неравенства.
Например, результат сравнения частных 1800:48 и 2100:60 можно записать в виде неравенства: 1800:48 > 2100:60.
Если выражения содержат переменные, то для разных значений переменных результат сравнения значений этих выражений может оказаться различным.
Решим задачу: "Пшеницей засеяли два опытных участка площадью 48 и 60 га. С первого участка собрали 180 ц пшеницы, а со второго 2100 ц. На каком участке урожайность выше?"
Урожайность выражается частным от деления массы пшеницы, собранной с участка, на площадь участка. Чтобы узнать, на каком участке урожайность выше, надо сравнить значения выражений 1800:48 и 2100:60. Так как 1800:48=37,5; 2100:60=35, то урожайность выше на первом участке.
Сравним, например, значения выражений 2a и a+4 при a=0, 4, 10.
Если a=0,то 2a=0 и a+4=4, т. е. при a=0 верно неравенство 2a< a+4.
Если a=4, то 2a=8 и a+4=8, т. е. при a=4 верно равенство 2a=a+4.
Если a=10, то 2a=20 и a+4=14, т. е. при a=10 верно неравенство 2a>a+4.
Иногда требуется установить, между какими числами заключено значение выражения.
Рассмотрим пример. Пусть при взвешивании металлического шарика установили, что его масса больше 86 г, но меньше 87г. Обозначим массу шарика (в граммах) буквой m. Тогда результат взвешивания можно записать так:
m>86 и m<87
или иначе:
86<m и m<87.
Два неравенства 86<m и m<87 можно записать в виде двойного неравенства
86<m<87.
Неравенство 86<m<87 читают так: "86 меньше m и m меньше 87"-или короче: "m больше 86 и меньше 87".
Рассмотрим ещё один пример. Число дней в месяце меньше 31 или равно 31. Обозначим число дней в месяце буквой n. Тогда n<31 или n=31.
Вместо этой записи обычно пишут одно неравенство n≤31 (читают:"n меньше или равно 31").
Число дней в месяце больше или равно 28: n>28 или n=28.
В таких случаях также пишут короче n≥28 (читают:"n больше или равно 28"). Так как n≥28, то 28≤n. Два неравенства
28≤n и n≤31
можно записать в виде двойного неравенства
28≤n≤31.
Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков ≥ и ≤, называют нестрогими.
Основные свойства сложения и умножения чисел.
Переместительное свойство сложения: от перестановки слагаемых значение суммы не меняется. Для любых чисел a и b верно равенство
a+b=b+a
Сочетательное свойство сложения: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего. Для любых чисел a, b и c верно равенство
(a+b)+c=a+(b+c)
Переместительное свойство умножения: от перестановки множителей значение произведения не изменяется. Для любых чисел а, b и c верно равенство
ab=ba
Сочетательное свойство умножения: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
Для любых чисел а, b и c верно равенство
(ab)c=a(bc)
Распределительное свойство: чтобы умножить число на сумму, можно умножить это число на каждое слагаемое и сложить полученные результаты. Для любых чисел a, b и c верно равенство
a(b+c)=ab+ac.
Из переместительного и сочетательного свойств сложения следует: в любой сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.
Пример 1 Вычислим сумму 1,23+13,5+4,27.
Для этого удобно объединить первое слагаемое с третьим. Получим:
1,23+13,5+4,27=(1,23+4,27)+13,5=5,5+13,5=19.
Из переместительного и сочетательного свойств умножения следует: в любом произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.
Пример 2 Найдём значение произведения 1,8·0,25·64·0,5.
Объединив первый множитель с четвёртым, а второй с третьим, будем иметь:
1,8·0,25·64·0,5=(1,8·0,5)·(0,25·64)=0,9·16=14,4.
Распределительное свойство справедливо и в том случае, когда число умножается на сумму трёх и более слагаемых.
Например, для любых чисел a, b, c и d верно равенство
a(b+c+d)=ab+ac+ad.
Мы знаем, что вычитание можно заменить сложением, прибавив к уменьшаемому число, противоположное вычитаемому:
a-b=a+(-b).
Это позволяет числовое выражение вида a-b считать суммой чисел a и -b, числовое выражение вида a+b-c-d считать суммой чисел a, b, -c, -d и т. п. Рассмотренные свойства действий справедливы и для таких сумм.
Пример 3 Найдём значение выражения 3,27-6,5-2,5+1,73.
Это выражение является суммой чисел 3,27, -6,5, -2,5 и 1,73. Применив свойства сложения, получим: 3,27-6,5-2,5+1,73=(3,27+1,73)+(-6,5-2,5)=5+(-9) =-4.
Пример 4 Вычислим
произведение 36·(![]() ).
).
Множитель ![]() можно рассматривать как сумму чисел
можно рассматривать как сумму чисел ![]() и -
и -![]() .
Используя распределительное свойство умножения, получим:
.
Используя распределительное свойство умножения, получим:
36(![]() )=36·
)=36·![]() -36·
-36·![]() =9-10=-1.
=9-10=-1.
Определение. Два выражения, соответственные значения которых равны при любых значениях переменных, называются тождественно равными.
Определение. Равенство, верное при любых значениях переменных, называется тождеством.
Найдём значения выражений 3(x+y) и 3x+3y при x=5, y=4:
3(x+y)=3(5+4)=3·9=27,
3x+3y=3·5+3·4=15+12=27.
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных соответственные значения выражений 3(x+y) и 3x+3y равны.
Рассмотрим теперь выражения 2x+y и 2xy. При x=1, y=2 они принимают равные значения:
2x+y=2·1+2=4;
2xy=2·1·2=4.
Однако можно указать такие значения x и y, при которых значения этих выражений не равны. Например, если x=3, y=4, то
2x+y=2·3+4=10,
2xy=2·3·4=24.
Выражения 3(x+y) и 3x+3y являются тождественно равными, а выражения 2x+y и 2xy не являются тождественно равными.
Равенство 3(x+y)=x+3y, верное при любых значениях x и y, является тождеством.
Тождествами считают и верные числовые равенства.
Так, тождествами являются равенства, выражающие основные свойства действий над числами:
a+b=b+a, (a+b)+c=a+(b+c),
ab=ba, (ab)c=a(bc), a(b+c)=ab+ac.
Можно привести и другие примеры тождеств:
a+0=a, a+(-a)=0, a-b=a+(-b),
a·1=a, a·(-b)=-ab, (-a)(-b)=ab.
Замену одного выражения другим, тождественно равным ему выражением называют тождественным преобразованием или просто преобразованием выражения.
Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.
Чтобы найти значение выражения xy-xz при заданных значениях x, y, z, надо выполнить три действия. Например, при x=2,3, y=0,8, z=0,2 получаем:
xy-xz=2,3·0,8-2,3·0,2=1,84-0,46=1,38.
Этот результат можно получить, выполнив лишь два действия, если воспользоваться выражением x(y-z), тождественно равным выражению xy-xz:
xy-xz=2,3(0,8-0,2)=2,3·0,6=1,38.
Мы упростили вычисления, заменив выражение xy-xz тождественно равным выражением x(y-z).
Тождественные преобразования выражений широко применяются при вычислении значений выражений и решении других задач. Некоторые тождественные преобразования уже приходилось выполнять, например, приведение подобных слагаемых, раскрытие скобок. Напомним правила выполнения этих преобразований:
чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть;
если перед скобками стоит знак "плюс", то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки;
если перед скобками стоит знак "минус", то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки.
Пример 1 Приведём подобные слагаемые в сумме 5x+2x-3x.
Воспользуемся правилом приведения подобных слагаемых:
5x+2x-3x=(5+2-3)x=4x.
Это преобразование основано на распределительном свойстве умножения.
Пример 2 Раскроем скобки в выражении 2a+(b-3c).
Применив правило раскрытия скобок, перед которыми стоит знак "плюс":
2a+(b-3c)=2a+b-3c.
Проведённое преобразование основано на сочетательном свойстве сложения.
Пример 3 Раскроем скобки в выражении a-(4b-c).
Воспользуемся правилом раскрытия скобок, перед которыми стоит знак "минус":
a-(4b-c)=a-4b+c.
Выполненное преобразование основано на распределительном свойстве умножения и сочетательном свойстве сложения. Покажем это. Представим в данном выражении второе слагаемое –(4b-c) в виде произведения (-1)(4b-c):
a-(4b-c)=a+(-1)(4b-c).
Применив указанные свойства действий, получим:
a-(4b-c)=a+(-1)(4b-c)=a+(-4b+c)=a-4b+c.
- Управление процессом обучения на первых уроках
- Психолого-педагогический аспект
- Методика изучения числовых выражений
- Изучение сравнений значений выражений
- Изучение свойств действий над числами
- Методика изучения тождественных преобразований
Прочие статьи:
Выбор в основных психолого-педагогических концепциях
Появление в современном обществе свободы выбора – с одной стороны и постоянно меняющаяся социально-экономическая ситуация в стране, духовный хаос – с другой приводит к тому, что люди постоянно находятся в ситуации выбора. Это состояние свободы выбора и ответственности оказывается непривычным, диско ...
Обзор и интерпретация эмпирических данных
Результаты диагностики по выявлению роли эксперимента в экологическом образовании дошкольников представлены в таблицах, гистограммах. Данные по каждой методике представлены в числовом и процентном виде. Таблица 2. Экологическая образованность дошкольников на начало года Испытуемый Уровень сформиров ...
Социальные мотивы получения образования
Мотивация получения высшего образования зависит от различных факторов (гендерных, возрастных, специализации вуза и др.). Более того, можно предположить, что эти факторы действуют не изолированно друг от друга, а взаимосвязаны. Иными словами, можно попытаться выявить различные типы мотивации получен ...
Меню сайта
- Главная
- Методы обучения и система образования
- Экологическое воспитание младших школьников
- Детское движение в современном обществе
- Социальное сиротство
- Педагогические ошибки учителей
- Развитие педагогики в России
- Статьи об образовании

