Методика изучения числовых выражений

Статьи об образовании » Методика организации учебно-познавательной деятельности учащихся на первых уроках алгебры » Методика изучения числовых выражений

Страница 3

Решить №1 (а. в. д. ж. и. л) на доске и в тетрадях. Решить № 2 (б, в). Решить № 4 (а, в, е, и, к, л) на доске и в тетрадях. Решить № 5 (а, в, д, з).

Самостоятельно решить (с проверкой решения):

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ;

з) ; и) .

Повторение ранее изученного материала: решить № 16 на доске и в тетрадях.

Дополнительные задачи (см. приложение).

V. Итог урока.

Какую тему вы изучали?

Что называется числовым выражением?

Что называется значением числового выражения?

Приведите пример числового выражения и укажите, в каком порядке надо выработать действия, чтобы найти его значение.

Приведите пример числового выражения, не имеющего смысла.

Учитель оценивает ответы учащихся.

VI. Задание на дом.

п. 1 (выучить наизусть правила); № 5 (б, г, е, з), 17 (б, г, е) и 3.

Урок 3

Тема урока: Числовые выражения

Цели урока:

а) образовательная: повторить правила действий с обыкновенными и десятичными дробями и закрепить их знание в ходе выполнения упражнений. Знать, что выражение, содержащее действие деления на нуль, не имеет смысла. Закрепление и систематизация изученного материала; проверка усвоения учащимися изученного материала;

б) развивающая: развить навыки самостоятельной работы, логическое мышление, математические способности;

в) воспитывающая: воспитать чувство долга, ответственности.

Тип урока: Урок усвоения навыков и умений

Ход урока:

I. Проверка домашнего задания.

1. Проверить по тетрадям выполнение учащимися домашнего задания № 5 (б, г, е, з) и № 17 (б, г, е).

2. Вычислите (устно):

а) 0,52; б) (-7)2; в) (-0,1)3.

3. Имеет ли смысл выражение (устно):

а) б) ; в) .

Математические действия дают возможность разыграть настоящие алгебраические "комедии и фарсы" на такие сюжеты: 2=5, 2=3 и т. п.

Юмор подобных математических представлений кроется в том, что ошибка замаскирована и не сразу бросается в глаза.

Докажем, что 4=-4. На доске неоспоримое равенство:

16=16

(4)2=(-4)2

Представим числа 4 и -4 в виде суммы, т. е.

(1+3)2=(-6+2)2

Дальнейший ход "комедии" состоит в преобразованиях. Видим, что показатель степени один и тот же и выражения равны, следовательно, делаем вывод, что

1+3=-6+2,

но выполняя вычисления, получаем

4=-4.

В чём ошибка?

При фронтальной работе выясняется, в чём состоит ошибка. Учитель вместе с классом делает вывод, что с числовыми выражениями нужно работать аккуратно на основе правил выполнения действий и использовать свойства рациональных чисел, т. к. внешний вид часто бывает обманчив.

Если между двумя двойками знак сложения заменить знаком умножения, то результат не изменится. Действительно,

Нетрудно подобрать три числа, обладающие тем же свойством, а именно

Есть и четыре однозначных числа, сложив которые или умножив друг на друга, мы получим один и тот же результат.

Кто быстрее подберёт эти числа?

Можно найти 5, 6, 7 и т. д. однозначных чисел, обладающих тем же свойством. Имейте в виду, что начиная с группы в пять чисел, ответы могут быть различными.

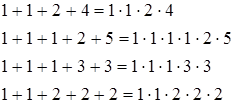
В математике таких ситуаций много; если вы найдёте ещё такие случаи, то можно разобрать их на следующем уроке.

II. Тренировочные упражнения:

Запишите в виде выражения:

а) сумму чисел 37,5 и 11,1;

б) произведение числа 7 и суммы чисел 11,4 и 12,6;

в) частное от деления разности чисел 47 и 12 на 5;

г) частное числа 13 и разности чисел 27 и 33;

д) сумму чисел -5 и произведения чисел 13 и -8.

Вычислите:

а)

б)

в)

Страницы: 1 2 3 4 5 6

Прочие статьи:

Методика изучения нумерации чисел младшими школьниками
При характеристике содержания и системы построения начального курса математики говорилось, что работа, направленная на формирование у детей понятия о числе и арифметических действиях, ведется в течение всех трех лет начального обучения и составляет основу всего курса. Программа предусматривает пост ...

Воспитание как общественное и педагогическое явление. Цели и ценности гуманистического воспитания
Воспитание – рассматривается в пед-ке в широком и в узком смысле. В широком – это передача исторического и культурного опыта от поколения к поколению. В узком – это целенаправленная деят-ть по формированию у детей системы качеств лич-ти, взглядов и убеждений. Воспитание яв-ся двусторонним процессом ...

Общее представление об учебной деятельности
При освоении любой деятельности человек приобретает определенные способности: например, в труде ребенок обретает способность к планированию, в игре - к воображению и действию в уме. В учебной деятельности ребенок обретает способность учить себя, или умение учиться. Умение учиться, формируемое в уче ...

Методика изучения числовых выражений

Меню сайта