Применение занимательного задачного материала на уроках математики

и

В заключении Бхаскара делает такое замечание: «Так как есть число отрицательное, то годится только первое решение».

Но комментатор Бхаскары Кришна Бхатта говорил, что если бы по условию вопроса было сказано: одна пятая часть стаи вычитается из трех, то второе решение, а не первое удовлетворяло бы условию.

3. Задача Магавиры:

Найти число павлинов в стае, которой, умноженная на себя, сидит на мандариновом дереве, а квадрат остатка вместе с 14 другими павлинами – на дереве тамала.

Решение: задача сводиться к решению квадратного уравнения

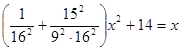, где x – число павлинов в стае.

Отсюда , а не подходит по смыслу задачи.

6. Задачи по теме «Алгебраические дроби» (8 класс)

1. Один путник идет от града в дом, а ходу его будет 17 дней, а другой путешественник от дому во град тот же путь творяше, может пройти в 20 дней, оба же сии человека пойдоша во един и тот же час от мест своих, и ведательно есть, в колико дней сойдуться? (Магницкий)

Решение: Пусть x – км весь путь, тогда км/дн – скорость первого, км/дн – скорость второго

км/дн – скорость сближения

дн

Ответ: встретятся через дней.

2. Задача Ньютона

Некий торговец каждый год увеличивает на одну треть свое состояние, уменьшенное на 100 фунтов, которые ежегодно затрачивает на свою семью. Через три года обнаруживает, что его состояние удвоилось. Спрашивается, сколько у него было денег вначале?

Решение Ньютона. «Чтобы решить вопрос, заметьте, что в нем содержатся в скрытом виде некоторые предложения, которые все должны быть выявлены и выражены».

Таким образом, вопрос выражается уравнением

приведя которое, мы найдем x

Умножьте уравнение на 27, и вы получите 64х-14800=54х,

Вычтите из обеих сторон 54х, и останется 10х-14800=0 или 10х=14800; разделив на 10, вы найдете, что х=14800. Т.о., состояние торговца вначале, а также его последующая прибыль, или доход, были равны 14800 фунтов.

3. Обмен зайцев на кур.

Крестьянин менял зайцев на кур: брал за всяких двух зайцев по три курицы. Каждая курица снесла яйца – третью часть от числа всех куриц. Крестьянин, продавая яйца, брал за каждые 9 яиц по столько копеек, сколько каждая курица снесла яиц, и выручил 72 копейки. Сколько было кур и сколько зайцев?

Решение: обозначим за x количество кур, которое выменял крестьянин.

Каждая курица снесла, как сказано в условии, яиц и общее число яиц у крестьянина составляет штук.

Каждые 9 яиц крестьянин продал по копейки, то есть одно яйцо за и выручил поэтому копеек, что по условию равно 72 копейки. Из равенства

Прочие статьи:

Виды вербальной агрессии
При описании основных видов вербальной агрессии мы использовали системный подход как позволяющий более точно определить природу того или иного проявления вербальной агрессии и выявить особенности его функционирования в изучаемой речевой среде. Виды речевой агрессии выделялись и описывались в форме ...

Цели и задачи внеучебной работы со студентами
Воспитание высоконравственной, духовно развитой и физически здоровой личности – гражданина России, способной к высококачественной профессиональной деятельности и моральной ответственности за принимаемые инженерно-технические и другие решения Формирование у студентов нравственных, духовных и культур ...

Методические особенности проведения детской экспериментальной деятельности
Организация экспериментальной деятельности ребенка, обеспечивающей его развитие, возможно при выполнении педагогом двух важных условий: стать реальным участником совместного поиска, а не только его руководителем, включиться в реальный, фактически осуществляемый ребенком эксперимент. Опыт всегда дол ...

Меню сайта

• Главная
• Методы обучения и система образования
• Экологическое воспитание младших школьников
• Детское движение в современном обществе
• Социальное сиротство
• Педагогические ошибки учителей
• Развитие педагогики в России
• Статьи об образовании