Применение занимательного задачного материала на уроках математики

8. Некто сказал своему другу: «Дай мне сто рупий, и я буду вдвое богаче тебя», на что последний ответил: «Если ты мне дашь только 10 рупий, я стану вшестеро богаче тебя». Спрашивается, сколько было у каждого?

Решение: Пусть у первого было рупий, а у второго рупий. Ясно, что первое условие будет выполнено. Имея в виду второе условие, находим

Следовательно, у первого было 140-100=40 рупий, у второго 70+100=170 рупий.

9. Купец, будучи должен 753 руб., попросил у того же заимодавца еще 303 руб. Последний согласился удовлетворить его просьбу на условии, чтобы весь долг был уплачен в течении 8 месяцев и притом так, чтобы должник, внеся к концу первого месяца некоторую сумму на покрытие части долга, ежемесячно увеличивал свой взнос на половину, т.е. уплатил бы во второй месяц полторы таких суммы, в третий месяц две таких же суммы, в четвертый две с половиной и т.д. Обсудив эти условия, купец согласился на них. Спрашивается, какую сумму должен он внести в первый месяц и сколько в каждый из следующих месяцев?

Решение:

Пусть к концу первого месяца купец должен внести x руб., тогда

(рублей)

2–ой месяц 48+24=72

3-ий месяц 48+48=96

4-ый месяц 48+48+24=120

5-ый месяц 48+48+48=144

6-ой месяц 48+48+48+24=168

7-ой месяц 48+48+48+48=192

8-ой месяц 48+48+48+48+24=216

10. Задача из «Курса алгебры» А.Н. Страннолюбского.

Два работника прожили у хозяина равное время; один из них получал по 15, а другой по 10 рублей в неделю. При окончательном расчете оказалось, что первый работник должен получить более второго именно на ту сумму, которую он забрал в течение работы, а забрал он сперва 4 руб., потом 3 руб., и наконец 7 рублей. Сколько продолжалась работа?

Решение:

Пусть x - число недель, в течении которых продолжалась работа, (15-10) разница в полученных деньгах, тогда:

(недели)

11. Отец завещал своего имения сыну и дочери; из оставшегося затем капитала 2500 руб. должны были пойти на уплату долга, а 3000 руб. в пользу вдовы. Как велик был оставленный отцом капитал и по скольку должны получить сын и дочь?

Решение: Обозначим оставленный отцом капитал через x, тогда

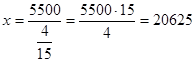(руб.)

Сыну завещал

Дочери завещал

12. Некто на вопрос о возрасте двух его сыновей отвечал: «Первый мой сын втрое старше второго, а обоим им вместе столько лет, сколько было бы мне 29 лет тому назад; мне теперь 45 лет». Найти лета обоих сыновей.

Решение: Обозначим лета второго сына через x, тогда

4 года второму сыну

А первому (лет)

13. Задача Магницкого

Спросил некто учителя: «Скажи, сколько у тебя в классе учеников, так хочу отдать тебе в учение своего сына». Учитель ответил: «Если придет еще учеников столько же, сколько имею, и пол столько, и четвертая часть, и твой сын, тогда у меня учеников 100». Спрашивается, сколько было у учителя учеников?

Решение:

I способ (стандартное решение)

Пусть было x учеников. Составим уравнение

; (учеников)

II способ

Эту задачу Магницкий решает «фальшивым правилом» (или методом «двух ложных положений»), которому в своей «Арифметике» отводит особое место.

Прочие статьи:

Основные направления деятельности педагога-психолога по коррекции нарушений социального развития дошкольников с ЗПР
Следующая задача нашего исследования – выделить комплекс игровых упражнений, направленных на формирование и коррекцию социального развития детей старшего дошкольного возраста с ЗПР. Игра – один из тех видов детской деятельности, которая используется взрослыми в целях воспитания дошкольников, обучая ...

Условия реализации, формы, средства и дидактические приемы, используемые в программе
Целью нашей системы оздоровления стало создание таких условий, которые помогут каждому ребенку стать телесно и психически здоровым, многогранно способным, радостным и счастливым. Для реализации данной программы в детском саду созданы следующие условия: · музыкально-физкультурный зал, оборудованный ...

Организация внеучебной работы на факультете естественных наук КГУ
Хотелось начать пафосно: «Внеучебная работа на факультете естественных наук "КГУ" осуществляется исходя из концепции, целей, задач, принципов, обозначенных в среднесрочной программе развития воспитательной работы в "КГУ" на период 2008-2009 гг., принятой на Ученом совете "К ...

Меню сайта

• Главная
• Методы обучения и система образования
• Экологическое воспитание младших школьников
• Детское движение в современном обществе
• Социальное сиротство
• Педагогические ошибки учителей
• Развитие педагогики в России
• Статьи об образовании