Применение занимательного задачного материала на уроках математики

1. Задача Евклида

Мул и осёл под вьюком, по дороге с мешками шагали. Жалобно охал осел, непосильною ношей придавлен. Это подметивший мул обратился к сопутчику с речью: «Что ж, старина, ты заныл и рыдаешь, будто девчонка? Нес бы вдвойне я, чем ты, если б отдал одну ты мне меру, если ж бы ты у меня лишь одну взял, то мы бы сравнялись». Сколько нес каждый из них, о геометр, поведай нам это.

Решение: I способ

Если x – груз мула, то (x-1) груз осла, увеличенный на, а следовательно, первоначальный груз осла был (x-2). С другой стороны, в два раза больше, чем груз осла, уменьшенный на 1, т.е. . Т.о.,

.

Отсюда, груз мула и груз осла 7-2=5.

II способ (через систему линейных уравнений)

Обозначив через x поклажу осла, а через y – поклажу мула, сводим задачу к системе уравнений с двумя неизвестными

Или

Груз мула y=7, груз осла x=5.

2. Задача Диофанта (из трактата «Арифметика»)

Найти три числа так, чтобы наибольшее превышало среднее на данную часть наименьшего, чтобы среднее превышало меньшее на данную часть наибольшего и чтобы наименьшее превышало число 10 на данную часть среднего числа.

Решение: Исходя из условий задачи, составим систему

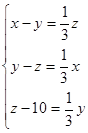
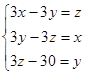
подставим 3-е уравнение в 1-е, получим

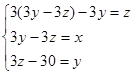
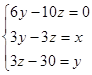
в первое уравнение вместо y подставим (3z-30), и рассмотрим только первое уравнение

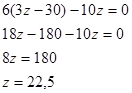
Подставим z в 3 уравнение и найдем y

И найдем x из второго уравнения

Ответ: , ,

3. Задача Китая, из трактата «Девять отделов искусства счета»

5 волов и 2 барана стоят таэлей, а 2 вола и 8 баранов стоят 8 таэлей. Сколько стоят отдельно вол и баран?

Решение: пусть x цена вола, а y – цена барана

Решение задачи сводиться к рассмотрению следующей системы уравнений

Следовательно, один вол стоит 2 таэля, а один баран таэля.

4. Задача из рассказа А.П. Чехова «Репетитор»

Купец купил 138 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное – 3 рубля?

Решение: I способ условие задачи сводится к системе

63 – аршин синего сукна, 75 аршин черного сукна.

II способ Пусть синего сукна было x аршин, тогда черного аршин.

X=63 (аршина) – синего

138-63=75 (аршин) – черного.

Ответ: синего 63 аршина, черного 75 аршин.

5. Задача Леонардо Пизанского

Один говорит другому: «Дай мне 7 динариев, и я буду в 5 раз богаче тебя». А другой говорит: «Дай мне 5 динариев, и я буду в 7 раз богаче тебя». Сколько у каждого?

Прочие статьи:

Педагогическая антропология как наука
Чрезмерное обилие разнообразной информации, полученной антропологами во всех концах света, привело как к дифференциации внутри самой науки о происхождении видов, вычленению из нее самостоятельных научных направлений, так и к возрастанию интереса к человеку со стороны других гуманитарных наук и возн ...

Преодоление задержки речевого развития у детей раннего возраста
В диагностическую группу детского сада компенсирующего вида принимаются дети 2-4 лет с сохранным интеллектом, имеющие задержку речевого развития разной этиологии. Экспрессивная речь у них представлена в виде отдельных звукоподражаний, аморфных слов-корней, усеченных фраз или коротких малопонятных п ...

Выявление нарушений оптико – пространственных функций у младших школьников с оптической дисграфией
Экспериментальное изучение проводилось с сентября по декабрь 2004 года на базе общеобразовательной школы № 4 п. Кундур с учащимися 1-2 классов. Исследование проводилось в несколько этапов, констатирующий, формирующий, контрольный в количестве 20 человек. 1 этап констатирующий, цель данного этапа: р ...

Меню сайта

• Главная
• Методы обучения и система образования
• Экологическое воспитание младших школьников
• Детское движение в современном обществе
• Социальное сиротство
• Педагогические ошибки учителей
• Развитие педагогики в России
• Статьи об образовании