Применение занимательного задачного материала на уроках математики

Решение: условие задачи сводиться к системе

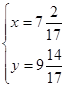
Следовательно, первый имел динария, а второй - динария.

6. Задача из сказки «1001 ночь» (ночь 458)

Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другая расположилась под деревом. Сидевшие на ветвях голуби говорят расположившимся внизу: «Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один ин нас слетел к вам, то нас с вами стало бы поровну». Сколько голубей сидело на ветвях и сколько под деревом?

Решение: если x и y – число голубей на дереве и под деревом, то по условию имеем

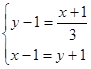
Ответ: 5 голубей на дереве и 3 голубя под деревом.

7. Задача Адама Ризе

Трое торгуют лошадь за 12 флоринов, но никто в отдельности не располагает такой суммой. Первый говорит двум другим: «Дайте мне каждый по половине своих денег, и я куплю лошадь». Второй говорит первому и третьему: «Дайте мне по одной трети ваших денег, и я приобрету лошадь». Наконец, третий говорит первым двум: «Дайте мне только по четвертой ваших денег, и лошадь будет моя». Теперь спрашивается, сколько денег было у каждого?

Решение: Пусть x, y, z – количество флоринов соответственно у первого, второго и третьего покупателей. Составим систему

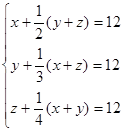
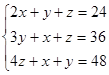
Выразим в первом уравнении и подставим во второе уравнение

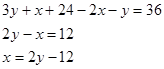
Теперь поставим x в первое уравнение, получим

Подставим x и z в третье уравнение и найдем y

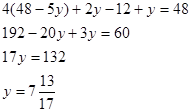
Зная y, найдем x и z.

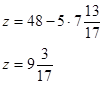
Ответ: , , – количество флоринов соответственно у первого, второго и третьего покупателей.

5. Задачи, решаемые с помощью составления квадратных уравнений

Для решения представленных здесь задач учащиеся должны предварительно уметь:

решать неполные квадратные уравнения;

решать полные квадратные уравнения;

решать приведенные квадратные уравнения;

находить ошибки в решенных уравнениях и исправлять их;

делать проверку.

1. Задача Бхаскары:

На две партии разбившись,

Забавлялись обезьяны.

Часть восьмая их в квадрате

В роще весело резвилась.

Криком радостным двенадцать

Воздух свежий оглашали.

Вместе сколько, ты скажешь,

Обезьян там было в роще?

Решение: если обозначим число всех обезьян через x, то задача сводится к решению квадратного уравнения

Прибавляя к обеим частям квадрат 32, будем иметь

После извлечения квадратного корня найдем

В данном случае, говорит Бхаскара, отрицательные единицы первой части таковы, что единицы второй части меньше их, а потому последнее можно считать и положительными и отрицательными, и получаем двойное значение неизвестного: 48 и 16.

Стандартное решение квадратного уравнения:

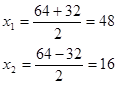
2. Задача Бхаскары

Сколько обезьян в стае, если квадрат пятой части, уменьшенной тремя, спрятался в пещере, и только одна осталась на виду, взобравшись на дерево?

Решение: задача сводиться к решению квадратного уравнения

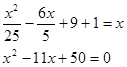
Прочие статьи:

Коррекционно-диагностическая программа для детей младшего дошкольного возраста с недоразвитием речи
Отправной точкой коррекционной программы является комплексное обследование педиатра, воспитателя, психолога, логопеда, дефектолога, рефлексотерапевта. Это служит базисом для организации командной работы этих специалистов. Благодаря ее преемственности снижается тяжесть социальной дезадаптации ребенк ...

Исследование и анализ работы учителей по изучению нумерации многозначных чисел в начальных классах
После изучения опыта работы мы решили провести исследование по данной проблеме непосредственно с учителями начальных классов. Для этого выбрали базой Яратовскую муниципальную основную общеобразовательную школу Баймакского района. Методы для исследования выбрали интервьюирование. Были включены в исс ...

Невербальные компоненты агрессивных высказываний
Системный подход к исследованию жанров, связанных с явлением речевой агрессии, предполагает анализ целого комплекса невербальных компонентов агрессивных высказываний. Основанием для этого является то, что эти компоненты в значительной степени определяют особенности функционирования вербальных прояв ...

Меню сайта

• Главная
• Методы обучения и система образования
• Экологическое воспитание младших школьников
• Детское движение в современном обществе
• Социальное сиротство
• Педагогические ошибки учителей
• Развитие педагогики в России
• Статьи об образовании